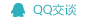路径规划是无人机实现高效、安全飞行的关键技术之一。Matlab 作为强大的科学计算和仿真软件，提供了丰富的工具和算法，为无人机路径规划提供了有力支持。下面深入讲解 Matlab 中用于无人机路径规划的常见算法。

A算法是一种启发式搜索算法，结合了 Dijkstra 算法的广度优先搜索策略和最佳优先搜索的启发式信息。它通过一个评估函数f(n)=g(n)+h(n)来选择下一个扩展节点，其中g(n)表示从起点到当前节点n的实际代价，h(n)是从当前节点n到目标节点的估计代价。在搜索过程中，A算法总是选择f(n)值最小的节点进行扩展，从而朝着目标节点快速搜索。

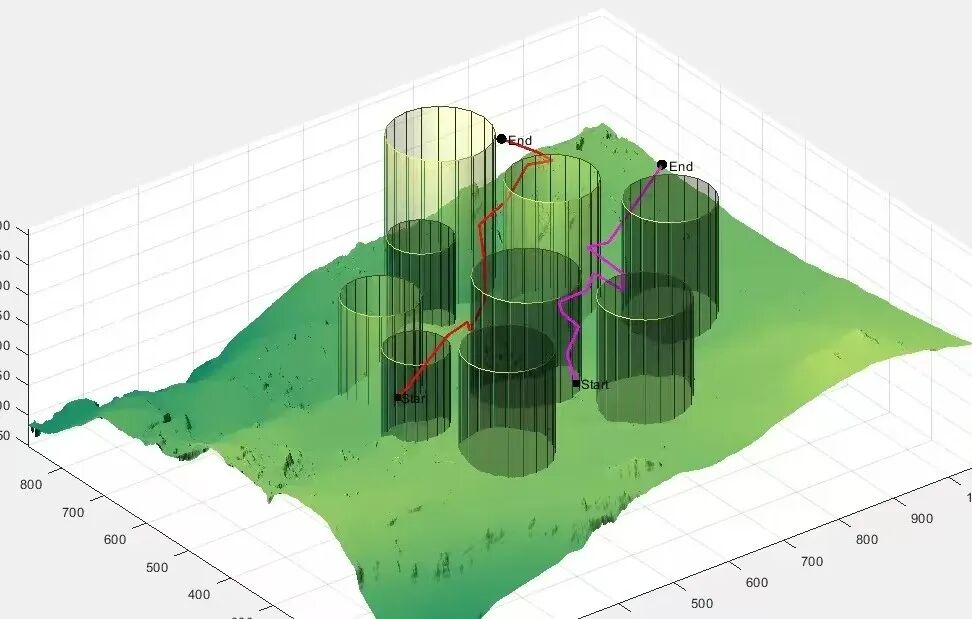
（二）在无人机路径规划中的应用

在无人机路径规划场景中，g(n)可以是无人机从起点飞行到当前节点所消耗的能量、时间或距离等实际代价。h(n)则可以根据当前节点与目标节点的欧几里得距离或其他距离度量方式来估计。例如，当无人机需要在一个存在障碍物的环境中从 A 点飞到 B 点时，A * 算法会不断评估每个可能的飞行节点，选择代价最小的路径前进，避开障碍物，最终找到从 A 到 B 的最优或近似最优路径。

（三）优缺点

优点是在大多数情况下能够快速找到最优路径，并且在搜索过程中利用启发式信息，避免了盲目搜索，大大提高了搜索效率。缺点是其性能依赖于启发函数的设计，如果启发函数不准确，可能导致搜索效率下降甚至无法找到最优解。同时，在复杂环境下，当障碍物较多时，搜索空间增大，计算量也会显著增加

（一）算法原理

Dijkstra 算法是一种典型的单源最短路径算法，用于计算一个节点到其他所有节点的最短路径。它采用贪心策略，从起点开始，每次选择距离起点最近且未被访问过的节点，更新其邻接节点的距离，直到所有节点都被访问过。

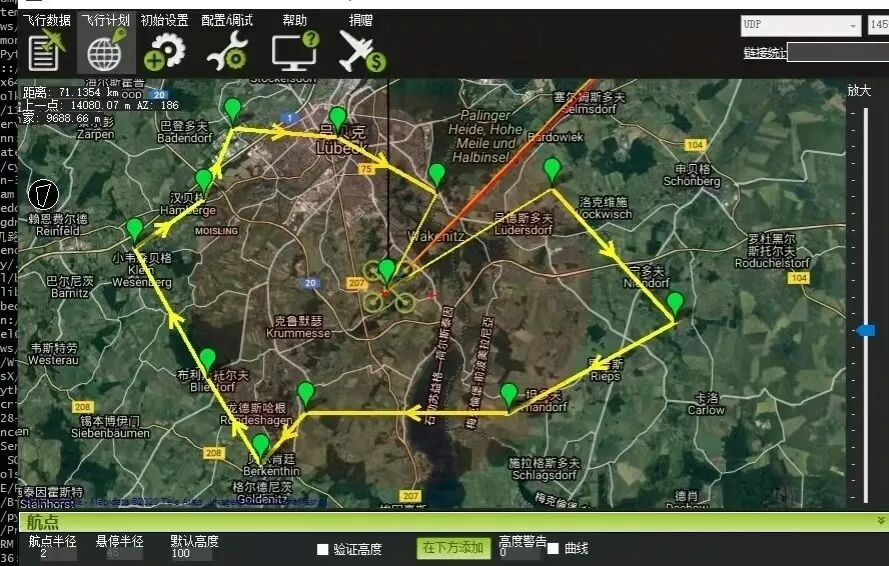
（二）在无人机路径规划中的应用

在无人机路径规划中，Dijkstra 算法将无人机的飞行区域抽象为一个图，节点代表无人机可能的位置，边代表节点之间的连接，边的权重可以表示飞行的代价，如距离、时间或能量消耗。通过该算法，无人机可以计算出从当前位置到目标位置的最短飞行路径。例如，在一个相对简单的飞行区域，没有复杂的障碍物分布，无人机可以利用 Dijkstra 算法快速计算出最短的飞行路线，以节省飞行成本。

（三）优缺点

优点是能够准确找到最短路径，且算法稳定可靠。缺点是它是一种广度优先搜索算法，在搜索过程中会遍历大量节点，计算复杂度较高，特别是在大规模的搜索空间中，计算时间会显著增加。而且它不考虑启发式信息，在复杂环境下搜索效率相对较低。

（一）算法原理

蚁群算法是一种模拟蚂蚁群体行为的启发式优化算法。蚂蚁在寻找食物的过程中会在路径上留下信息素，信息素浓度越高的路径，被其他蚂蚁选择的概率越大。随着时间的推移，较优路径上的信息素会不断积累，最终形成一条从蚁巢到食物源的最优路径。

（二）在无人机路径规划中的应用

在无人机路径规划中，将无人机看作蚂蚁，飞行路径看作蚂蚁的行走路径。无人机在飞行过程中，根据路径上的信息素浓度选择下一个飞行方向。同时，无人机在完成一次飞行后，会在其飞行路径上释放信息素，更新路径上的信息素浓度。例如，在一个复杂的城市环境中，存在多个禁飞区和障碍物，蚁群算法可以通过信息素的不断更新和积累，帮助无人机找到一条避开禁飞区和障碍物，同时满足飞行要求的优化路径。

（三）优缺点

优点是具有较强的鲁棒性和全局搜索能力，能够在复杂环境中找到较优路径。它不需要对问题有深入的了解，只需要根据信息素的反馈进行搜索。缺点是算法初期搜索速度较慢，因为信息素的积累需要一定时间。而且算法参数的选择对结果影响较大，需要进行合理的调整。

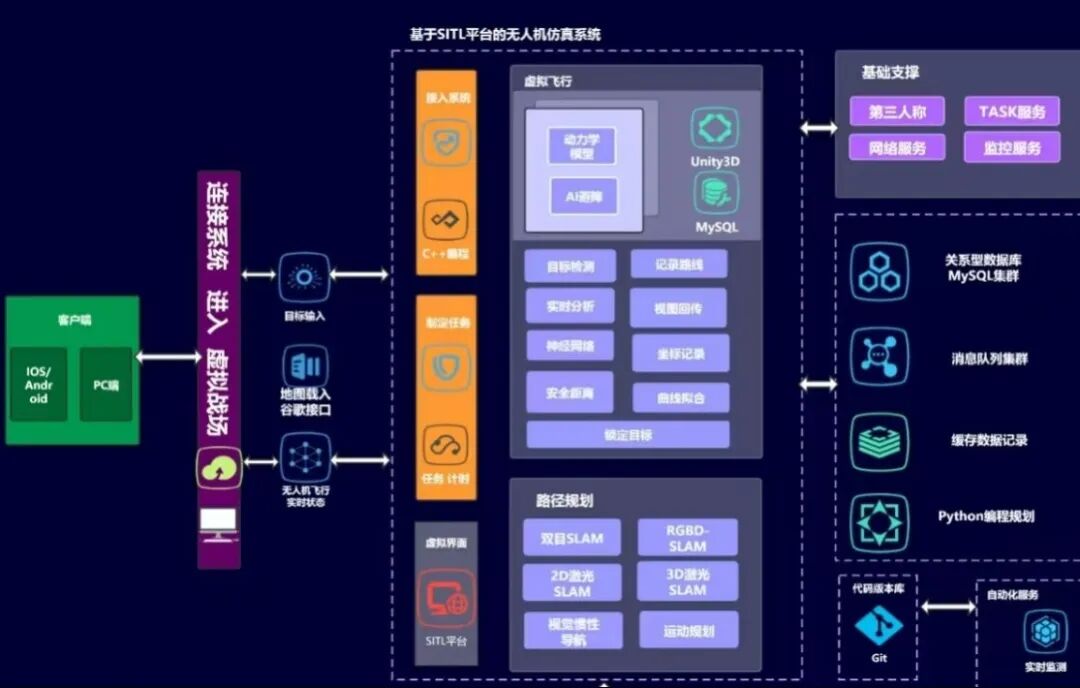
Matlab 提供了丰富的函数库和工具箱，方便实现这些路径规划算法。例如，Matlab 的 Robotics System Toolbox 中包含了用于路径规划的函数和工具，用户可以利用这些工具快速搭建无人机路径规划模型，进行算法的测试和优化。同时，Matlab 强大的绘图功能可以直观地展示路径规划的结果，便于分析和调试。

2025-09-27

326

分享到: 新浪微博 微信

分享到微信 ×

打开微信,使用扫一扫即可将网页分享至朋友圈。